
 |
Print Close |




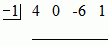
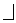 ' and then list the coefficients in a row. Remember that 4x3 – 6x + 1 = 4x3 + 0x2 – 6x + 1. Don't forget the 0 coefficient of x2. Now put a line under it as shown above.
' and then list the coefficients in a row. Remember that 4x3 – 6x + 1 = 4x3 + 0x2 – 6x + 1. Don't forget the 0 coefficient of x2. Now put a line under it as shown above.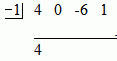
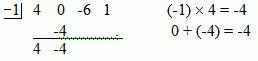
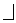 ' by the number under the line. Place the product under the second coefficient and then add down. Place the sum of the two numbers below the line as shown above.
' by the number under the line. Place the product under the second coefficient and then add down. Place the sum of the two numbers below the line as shown above.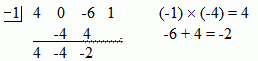
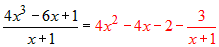



Copyright 2001- Castle Software, Inc. All Rights Reserved