Reference Tables for Geometry



List of Reasons for Geometric Proofs
- A median divides a line segment into two congruent line segments.
- A midpoint divides a line segment into two congruent line segments.
- A segment bisector divides a line segment into two congruent line segments.
- A perpendicular bisector divides a line segment into two congruent line segments.
- A perpendicular bisector creates congruent right angles.
- An altitude creates congruent right angles.
- An angle bisector divides an angle into two congruent angles.
- Two intersecting lines form congruent vertical angles.
- Two parallel lines cut by a transversal create congruent alternate interior angles.
- Two parallel lines cut by a transversal create congruent alternate exterior angles.
- Two parallel lines cut by a transversal create congruent corresponding angles.
- Isosceles triangles have two congruent sides.
- Isosceles triangles have two congruent base angles.
- All right angles are congruent.
- Perpendicular lines form congruent right angles.
- SAS
 SAS
SAS
- SSS
 SSS
SSS
- AAS
 AAS
AAS
- HL
 HL
HL
- ASA
 ASA
ASA
- AA
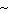 AA
AA
- Opposite sides of a parallelogram are congruent
- Opposite angles of a parallelogram are congruent
- Opposite sides of a parallelogram are parallel.
- CPCTC
- Reflexive Property
- Substitution Postulate
- Subtraction Postulate
- Addition Postulate
- Right triangles contain only one right angle.
- Corresponding parts of similar triangles are in proportion.
- The product of the means is equal to the product of the extremes.



Copyright 2001- Castle Software, Inc. All Rights Reserved


 SAS
SAS SSS
SSS AAS
AAS HL
HL ASA
ASA AA
AA